As explained in this article⁴, there are three simple rules for a valid pattern

1. The pattern must connect at least four points
2. A point should be used once at most in the pattern
3. An intermediate point becomes a contact point, unless it has already been connected before

Rules 1. and 2. imply that there should be at least one direction change in the pattern, so you cannot have obvious patterns like a straight line. However rule 3. is the most interesting because… sorry what? Oh, don't worry! It is a simple rule too, here is a graphical explanation.

The rule tells you have to always include points you cross on your path, unless they have already been included before. This is what I mean by "intermediate" point. Now, the interesting part of this rule is in how complex it makes the mathematical derivation of the number of possible patterns.

Let's ignore Rule 3. at first. With this simplification, a pattern connecting k points is equivalently a permutation of those k points taken from all the nine available points. A permutation is obtained by choosing in order k points from a bag containing 9 points. The number of different permutations is \[ P_k^n = 9\times 8 \times \dots \times (9 - k) = \frac{9!}{(9-k)!} \] We can then derive the total number of patterns by summing all patterns with 4 or more points (Rule 1.). \[ N_{\text{without Rule 3.}} = \sum_{k=4}^{9} \frac{9!}{(9-k)!} = 985824 \]

Now let's consider Rule 3., and think about what it changes. We now have to consider invalid permutations which should be subtracted from the total. This is manageable for patterns with 1,2 or 3 points, but it gets a lot harder for longer patterns. This complexity can be overcome by using a brute force algorithm which will test all patterns and count valid ones. Let's use Python code.

In our code, we label each point using a digit.

INTERMEDIATE_POINT = {
"13": "2",
"46": "5",
"79": "8",

"17": "4",
"28": "5",
"39": "6",

"19": "5",
"37": "5"
}

How do we know a given pattern is valid? Let's code a function that does that.

def is_pattern_valid(pattern):
    """We suppose the pattern is composed of unique characters. Returns True if no intermediate point is passed over, False otherwise."""
    for sequence, point in INTERMEDIATE_POINT.items():
        if sequence in pattern or sequence[::-1] in pattern:
            if point not in pattern or pattern.index(point) > pattern.index(sequence[0]):
                return False
    return True

We have all we need to code the main algorithm. I consider using a recursive function to be the most natural choice. There are two stopping conditions to recursion:

1. If the pattern is invalid
2. If the pattern has maximum length, that is, it contains all points (because of Rule 2.)

We keep track of a variable count to count the number of valid patterns we found, and the recursive call is made on the pattern augmented with one point from the available points.

def count_patterns(pattern="", points="123456789", max_length=9, min_length=4):
    # First, check Rule 3.
    if is_pattern_valid(pattern):
        count = 0
        if len(pattern) >= min_length:
            # Application of Rule 1.
            count += 1
        if len(pattern) == max_length or len(points) == 0:
            # Stopping condition 2.
            return count
        else:
            for p in points:
                # Recursive call following Rule 2.
                count += count_patterns(pattern + p, points.replace(p, ""),
                           max_length=max_length, min_length=min_length)
            return count
    else:
        # Stopping condition 1.
        return 0

Let's run it.

count_patterns("", "123456789", max_length=9, min_length=4)

This outputs 389,112. This confirms the result from the paper!

The following code is to demonstrate the impact of Rule 3. on the effective number of patterns. I print and plot the number of patterns by the number of connected points.

import math
import matplotlib.pyplot as plt

all_permutations = []
valid_patterns = []
n_points = range(1, 10)
for k in n_points:
 all_permutations.append(math.perm(9, k))
 valid_patterns.append(count_patterns(max_length=k, min_length=k))


plt.plot(n_points, valid_patterns, label="Valid patterns")
plt.plot(n_points, all_permutations, label="Permutations")
plt.ylabel('Patterns/Permutations')
plt.xlabel('Points in pattern/permutation')
plt.legend()
plt.show()

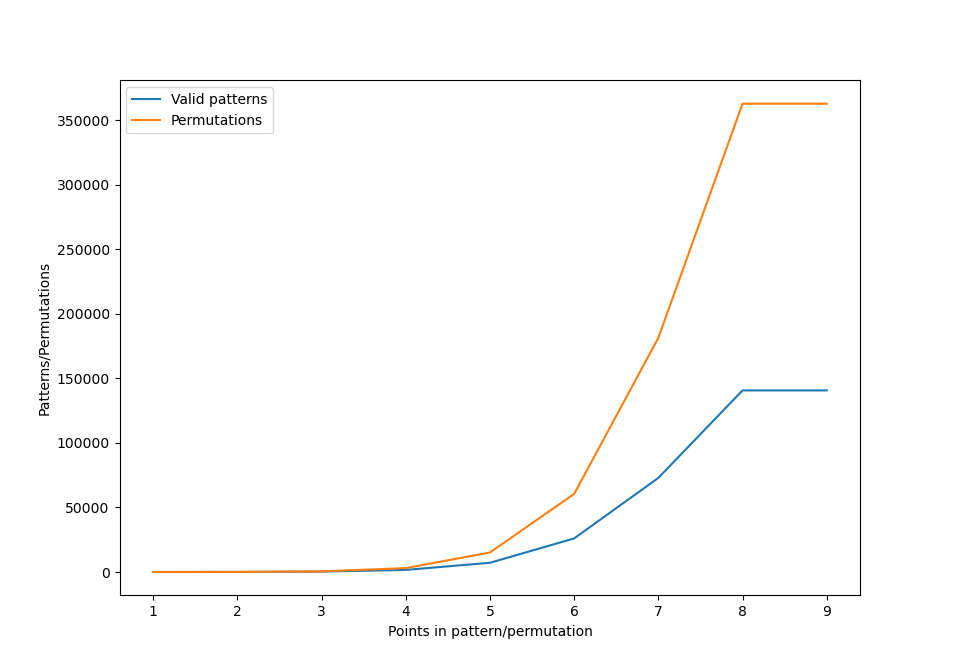
This last graph shows the number of patterns connecting the same given number of dots. So if you sum them all, you should obtain the number of total patterns that we computed. Remember to discard patterns with less than 3 dots and you get the number 389,112 for the blue line. We can also notice that the number of 8-dot patterns is the same as 9-dot patterns how is that so? Well, since there are only 9 dots available, when we have joined 8 dots together, there is only one remaining to form a 9-dot pattern, so in practical, 8-dot patterns are equivalent to 9-dot patterns.

And this concludes our short journey. That was some fun play with statistics! What do you think?